CLASIFICACIÓN Y PROPIEDADES DE LOS NÚMEROS REALES
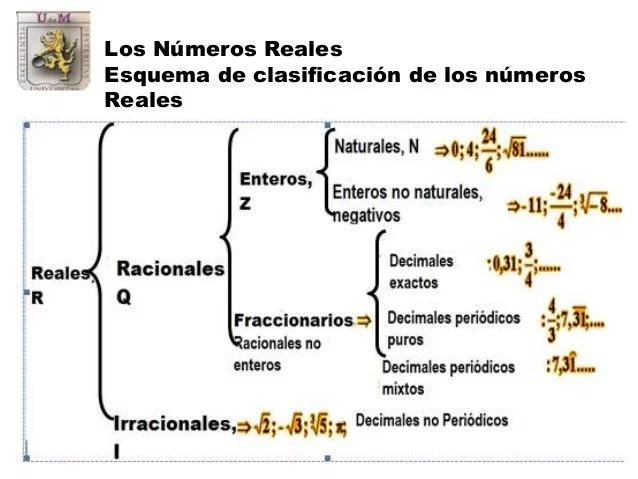
Los números reales son los que pueden ser expresados por un número entero o decimal.Esto quiere decir que abarcan a los números racionales pueden representarse como el cociente de dos enteros con denominador distinto a cero. Los números irracionales son que no pueden ser expresados como una fracción de números enteros con denominador diferente a cero. Los números naturales son aquellos que permiten contar los elementos de un conjunto. Los números enteros abarcan a los números naturales (los que se utilizan para contar los elementos de un conjunto), incluyendo al cero y a los números negativos (que son el resultado de restar a un número natural otro mayor). Por lo tanto, los números enteros son aquellos que no tienen parte decimal.
PROPIEDADES DE CAMPO DE LOS NÚMEROS REALES
Operaciones binarias de adición y multiplicación, por las cuales a cada pareja de núemeros reales se les asocia un número real llamados suma(+) y producto (x), respectivamente, y que además esta familiarizado con el uso del simbolo igual (=).
OPERACIONES CON NUMEROS REALES
Se realizan operaciones con numeros reales de manera fundamental con enteros y racionales.
LEY DE LOS SIGNOS
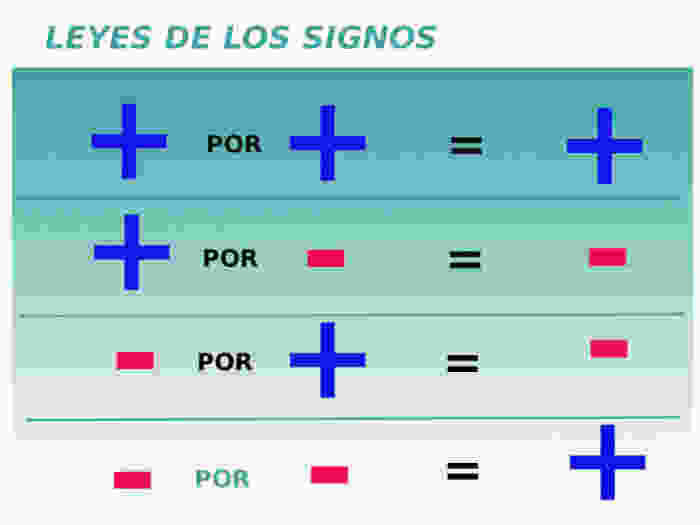
LEY DE LOS EXPONENTES
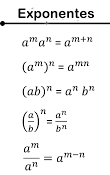
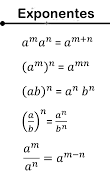
JERARQUÍA DE OPERACIONES
El orden en el que se ejecutan las operaciones es el siguiente potencias y raices, multiplicaciones y divisiones, el orden en el que se indiquen y sumas y restas.
Radicales
La radicación es la operación inversa de la potenciación. Si una potencia es:
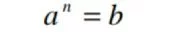La radicación es la operación que tiene que obtener aconociendo b y n. Se expresa:
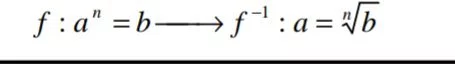Un radical puede llevar coeficientes que formen parte de el como por ejemplo: 3^n√ b
donde 3 es el coeficiente y forma parte del radical.
Si n = 2, es la raíz cuadrada y se acostumbra a omitir el índice
Si n = 3, es la raíz cúbica
Si n = 4, es la raíz cuarta y así sucesivamente.
Como consecuencia de las reglas sobre los signos de las potencias de exponente
natural y base negativa tenemos que:
• Toda raíz de índice impar de un número tiene el mismo signo que el radicando, ejemplo:
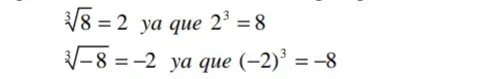•Toda raíz de índice par de un número positivo tiene doble signo, ejemplo:
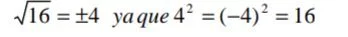•Toda raíz de índice par y radicando negativo no es real, ejemplo:
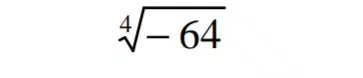Simplificación De Radicales Para simplificar un radical se divide el índice del radical y el exponente del
radicando por sus factores comunes (por el m.c.d).
Ejemplos:
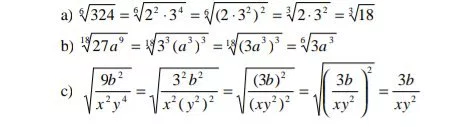Potenciación de un exponente fraccionario una potencia de exponente fraccionario es equivalente a un radical cuyo índice es el denominador del exponente y cuyo radicando es la base elevada al numerador del exponente
Ejemplo:
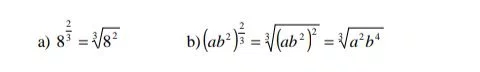Cociente de radicales de igual índice el cociente de radicales de igual índice es otro radical que tiene el mismo índice y por radicando el cociente de los radicandos.
1) Si los radicales no tienen igual índice se reducen previamente a índice común.
Ejemplo:
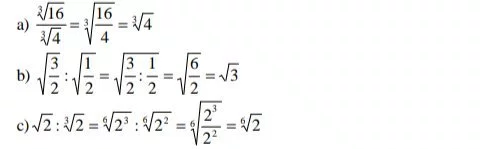2)Para extraer factores de un radical con radicando en forma de fracción se realiza primero el cociente de radicales y después se extraen independientemente losfactores del numerador y del denominador.
Ejemplo:
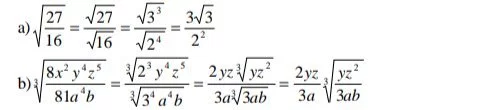Raíz De Un RadicalEjemplo:
1)La raíz n-ésima de la raíz n-ésima de un número es la raíz n-ésima de dicho número.Ejemplo:
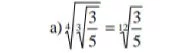
Media, Mediana Y Moda
Medidas De Dispersión
Media:
La media de un conjunto de números, algunas ocasiones simplemente llamada el promedio , es la suma de los datos dividida entre el número total de datos.
Ejemplo:
Encuentre la media del conjunto {2, 5, 5, 6, 8, 8, 9, 11}.
Hay 8 números en el conjunto. Súmelos, y luego divida entre 8.
M: 6.75
Mediana:
Encuentre la mediana del conjunto {2, 5, 8, 11, 16, 21, 30}.
Hay 7 números en el conjunto, y estos están acomodados en orden ascendente. El número medio (el cuarto en la lista) es 11. Así, la mediana es 11.
Moda
La moda es el valor más frecuente
Ejemplo:
Calcular la moda de la siguiente serie de números: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
Lenguaje Algebráico
Álgebra:
Es la rama de las matemáticas que se caracteriza por el empleo de letras para representar números.
Las expresiones algebraicas se clasifican por monomios, binomios, trinomios y polinomios.
Un monomio es un número o producto de dos o más números.
Por ejemplo.
7,2x,mn,5xy y ¾ son monomios.
Cada uno de los números que al multiplicarse forman el término se llaman factores.
Cualquier factor o grupo de factores de un término es coeficiente del producto de los factores restantes.
Así en 3xy, 3 es el coeficiente numérico de xy, mientras que xy es el coeficiente literal de 3. Si hacemos referencia al coeficiente de un término generalmente consideramos al factor numérico que nos indica el número de sumandos iguales que han de tomarse en cuenta.
Polinomio
Cuando dos o más términos (monomios) se relacionan por los signos más (+) o menos (-) se forma una expresión algebraica que recibe el nombre de polinomio.
Al polinomio de dos términos se le llama binomio y al de tres trinomio. Los monomios pueden considerarse como polinomios de un solo término.
El grado de un término o monomio lo determina la suma de los exponentes de las literales que intervienen en él.
Leyes De Exponentes
Primera Ley:
El producto de dos potencias de la misma base (distinta de cero) es igual a la base elevada a la suma de los exponentes.
Segunda Ley:
La potencia de otra potencia de la misma base (distinta de cero) es igual a la base elevada al producto de los exponentes.
Tercera Ley:
La potencia de un producto es igual al producto de los dos factores elevados a la misma potencia.
Cuarta Ley:
Para elevar una fracción a un exponente, el numerador y el denominador se elevan a dicho exponente.
Quinta Ley.
El cociente de potencias de igual base es igual a la misma base elevada a la resta de los exponentes.
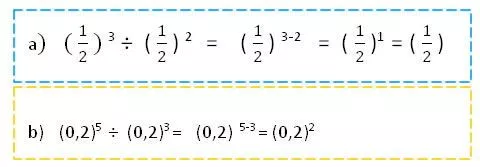
Desviación Media
Medidas De Dispersión
Como viste, el rango sólo considera dos datos: el dato mayor y el dato menor. Sin embargo, es conveniente contar con otra medida de dispersión de los datos respecto a la media en la que se tome en cuenta todas las observaciones
La desviación media es el promedio de las distancias (o diferencias) entre
todas las observaciones y la media aritmética. Se usa para medir la
variabilidad de un conjunto de datos y se calcula mediante la siguiente
ecuación:
Veamos un ejemplo:Hallar la desviación media de los siguientes datos:
2, 3, 6, 8, 11
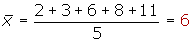Desviación media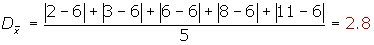
Números Y Operaciones Aritméticas
Clasificación Y Propiedades De Los Números Reales
El conjunto de los números reales lo empleamos de manera frecuente, sin embargo, cuando al lector se le pide que mencione cuáles son los números reales, surge lo que para él es un obstáculo.
Números naturales (N):
Los números naturales se denotan con el símbolo N y se definen así:
N: {1,2,3,…}
Donde los puntos suspensivos significan “y así sucesivamente”.
Con estos números se pueden efectuar las operaciones básicas como la suma, el
producto, la resta y la división.
Las primeras propiedades que los naturales tienen con respecto a las operaciones son las de cerradura y se cumplen para la suma y el producto, no así para la resta y la división.
Propiedades de cerradura para la suma y el producto de los números naturales
1. La suma de dos números naturales cualesquiera da como resultado un natural.
2. El producto de dos números naturales cualesquiera da como resultado un
natural.
Otras propiedades son la conmutatividad, la asociatividad y la distributiva.
Si consideramos que las letras
a b y c , representan a cualquier número natural, tenemos las siguientes propiedades escritas en forma verbal y en forma simbólica.
Propiedades conmutativas
3. El orden de los sumandos no altera la suma de números naturales.
a+b = b+a
4. El orden de los factores no altera el .producto de números naturales.
a•b = b•a
Propiedades asociativas
5. Para sumar tres o más números naturales no importa el orden.
a+b+c = a+b+c
6. Para realizar el producto de tres o más números naturales no importa el orden.
a•b•c = a•b•c
Propiedad distributiva
7. El producto de un número natural con la suma de dos naturales es igual a la
suma de los productos.
a• b+c = a• b+a• c
Números Enteros (Z)
Al restar dos números naturales el resultado no siempre da un natural, esto quiere decir
que la operación resta no cumple con la propiedad de cerradura, por ello es necesario utilizar “nuevos” números que vienen a complementar los naturales para que se satisfaga la cerradura en la resta, así como en la suma y el producto.
Dichos números se conocen como los Enteros, y son:
(Z)= …- 5, -4, -3, -2, -1,0,1,2,3,4,5,6,7,8,9,10…
Números racionales (Q)
Estos elementos son aquellos números que se pueden expresar como el cociente de dos números enteros, siendo el divisor diferente de cero.
Se denota por el símbolo (Q) y se define simbólicamente de la siguiente forma.
{Q= x tal que x= a/b donde a y b son enteros con b≠0}
Números Irracionales
Son aquellos cuya expresión decimal no es periódica.
Ejemplo de estos números es √2, √3, √5, √7 y en general la raíz cuadrada de un número primo, pues su expresión decimal no es periódica. También son números irracionales como el siguiente:
π: 3.1415926535…
Medidas De Dispersión
¿Qué son las medidas de tendencia central?
Estas dirigen su interés al comportamiento de los datos en relación a un valor central pero se olvidan de la forma en la que los datos varían o se dispersan.
¿Qué son las medidas de dispersión?
Las medidas de dispersión se encargan de estudiar el comportamiento de todos los datos y cómo se distribuyen alrededor de un valor central, la media aritmética. Dentro de las medidas de dispersión se encuentran: el rango, la desviación media, la desviación estándar y la varianza.
¿A qué se refiere el rango?
A la variación o diferencia entre el dato mayor y el dato menor de un conjunto de datos u observaciones se le llama Rango
Por ejemplo una serie de datos cuantitativas, como lo es la estatura, donde en centímetros tendríamos:
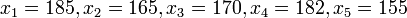Es posible ordenar los datos de la siguiente manera;
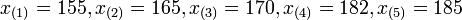Donde la notación x(i) indica que se trata del elemento i-ésimo de la serie de datos. De este modo, el rango sería la diferencia entre el valor máximo (k) y el mínimo; o, lo que es lo mismo:
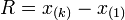En nuestro ejemplo, con cinco valores, nos da que R = 185-155 = 30.
PROPIEDADES DE CAMPO DE LOS NÚMEROS REALES
Operaciones binarias de adición y multiplicación, por las cuales a cada pareja de núemeros reales se les asocia un número real llamados suma(+) y producto (x), respectivamente, y que además esta familiarizado con el uso del simbolo igual (=).
OPERACIONES CON NUMEROS REALES
Se realizan operaciones con numeros reales de manera fundamental con enteros y racionales.
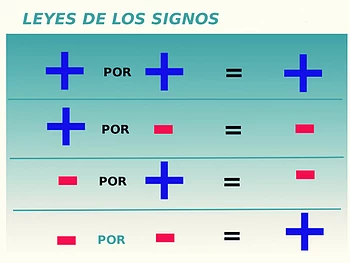
LEY DE LOS SIGNOS
LEY DE LOS EXPONENTES
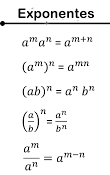
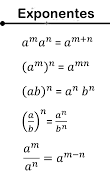
JERARQUÍA DE OPERACIONES
El orden en el que se ejecutan las operaciones es el siguiente potencias y raices, multiplicaciones y divisiones, el orden en el que se indiquen y sumas y restas.
Radicales
La radicación es la operación inversa de la potenciación. Si una potencia es:
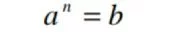La radicación es la operación que tiene que obtener aconociendo b y n. Se expresa: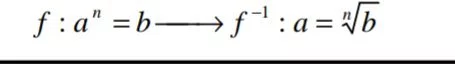Un radical puede llevar coeficientes que formen parte de el como por ejemplo: 3^n√ bdonde 3 es el coeficiente y forma parte del radical.
Si n = 2, es la raíz cuadrada y se acostumbra a omitir el índice
Si n = 3, es la raíz cúbica
Si n = 4, es la raíz cuarta y así sucesivamente.
Como consecuencia de las reglas sobre los signos de las potencias de exponente
natural y base negativa tenemos que:
• Toda raíz de índice impar de un número tiene el mismo signo que el radicando, ejemplo:
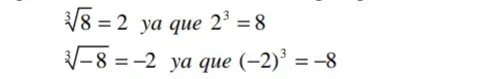•Toda raíz de índice par de un número positivo tiene doble signo, ejemplo: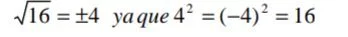•Toda raíz de índice par y radicando negativo no es real, ejemplo: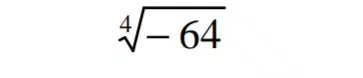Simplificación De Radicales Para simplificar un radical se divide el índice del radical y el exponente delradicando por sus factores comunes (por el m.c.d).
Ejemplos:
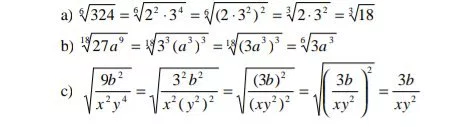Potenciación de un exponente fraccionario una potencia de exponente fraccionario es equivalente a un radical cuyo índice es el denominador del exponente y cuyo radicando es la base elevada al numerador del exponenteEjemplo:
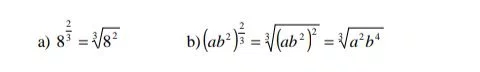Cociente de radicales de igual índice el cociente de radicales de igual índice es otro radical que tiene el mismo índice y por radicando el cociente de los radicandos.1) Si los radicales no tienen igual índice se reducen previamente a índice común.
Ejemplo:
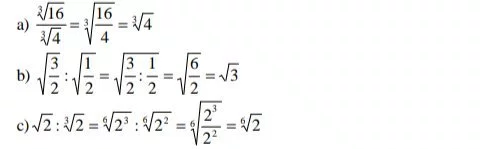2)Para extraer factores de un radical con radicando en forma de fracción se realiza primero el cociente de radicales y después se extraen independientemente losfactores del numerador y del denominador.Ejemplo:
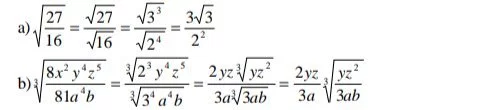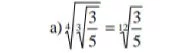
Raíz De Un RadicalEjemplo:1)La raíz n-ésima de la raíz n-ésima de un número es la raíz n-ésima de dicho número.Ejemplo:Media, Mediana Y Moda
Medidas De Dispersión
Media:
La media de un conjunto de números, algunas ocasiones simplemente llamada el promedio , es la suma de los datos dividida entre el número total de datos.
Ejemplo:
Encuentre la media del conjunto {2, 5, 5, 6, 8, 8, 9, 11}.
Hay 8 números en el conjunto. Súmelos, y luego divida entre 8.
M: 6.75
Mediana:
Encuentre la mediana del conjunto {2, 5, 8, 11, 16, 21, 30}.
Hay 7 números en el conjunto, y estos están acomodados en orden ascendente. El número medio (el cuarto en la lista) es 11. Así, la mediana es 11.
Moda
La moda es el valor más frecuente
Ejemplo:
Calcular la moda de la siguiente serie de números: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
Lenguaje Algebráico
Álgebra:
Es la rama de las matemáticas que se caracteriza por el empleo de letras para representar números.
Las expresiones algebraicas se clasifican por monomios, binomios, trinomios y polinomios.
Un monomio es un número o producto de dos o más números.
Por ejemplo.
7,2x,mn,5xy y ¾ son monomios.
Cada uno de los números que al multiplicarse forman el término se llaman factores.
Cualquier factor o grupo de factores de un término es coeficiente del producto de los factores restantes.
Así en 3xy, 3 es el coeficiente numérico de xy, mientras que xy es el coeficiente literal de 3. Si hacemos referencia al coeficiente de un término generalmente consideramos al factor numérico que nos indica el número de sumandos iguales que han de tomarse en cuenta.
Polinomio
Cuando dos o más términos (monomios) se relacionan por los signos más (+) o menos (-) se forma una expresión algebraica que recibe el nombre de polinomio.
Al polinomio de dos términos se le llama binomio y al de tres trinomio. Los monomios pueden considerarse como polinomios de un solo término.
El grado de un término o monomio lo determina la suma de los exponentes de las literales que intervienen en él.
Leyes De Exponentes
Primera Ley:
El producto de dos potencias de la misma base (distinta de cero) es igual a la base elevada a la suma de los exponentes.
Segunda Ley:
La potencia de otra potencia de la misma base (distinta de cero) es igual a la base elevada al producto de los exponentes.
Tercera Ley:
La potencia de un producto es igual al producto de los dos factores elevados a la misma potencia.
Cuarta Ley:
Para elevar una fracción a un exponente, el numerador y el denominador se elevan a dicho exponente.
Quinta Ley.
El cociente de potencias de igual base es igual a la misma base elevada a la resta de los exponentes.
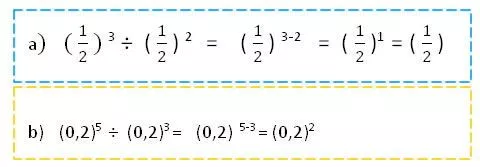
Desviación Media
Medidas De Dispersión
Como viste, el rango sólo considera dos datos: el dato mayor y el dato menor. Sin embargo, es conveniente contar con otra medida de dispersión de los datos respecto a la media en la que se tome en cuenta todas las observaciones
La desviación media es el promedio de las distancias (o diferencias) entre
todas las observaciones y la media aritmética. Se usa para medir la
variabilidad de un conjunto de datos y se calcula mediante la siguiente
ecuación:
Veamos un ejemplo:Hallar la desviación media de los siguientes datos:2, 3, 6, 8, 11
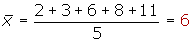Desviación media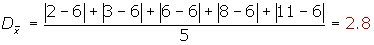Números Y Operaciones Aritméticas
Clasificación Y Propiedades De Los Números Reales
El conjunto de los números reales lo empleamos de manera frecuente, sin embargo, cuando al lector se le pide que mencione cuáles son los números reales, surge lo que para él es un obstáculo.
Números naturales (N):
Los números naturales se denotan con el símbolo N y se definen así:
N: {1,2,3,…}
Donde los puntos suspensivos significan “y así sucesivamente”.
Con estos números se pueden efectuar las operaciones básicas como la suma, el
producto, la resta y la división.
Las primeras propiedades que los naturales tienen con respecto a las operaciones son las de cerradura y se cumplen para la suma y el producto, no así para la resta y la división.
Propiedades de cerradura para la suma y el producto de los números naturales
1. La suma de dos números naturales cualesquiera da como resultado un natural.
2. El producto de dos números naturales cualesquiera da como resultado un
natural.
Otras propiedades son la conmutatividad, la asociatividad y la distributiva.
Si consideramos que las letras
a b y c , representan a cualquier número natural, tenemos las siguientes propiedades escritas en forma verbal y en forma simbólica.
Propiedades conmutativas
3. El orden de los sumandos no altera la suma de números naturales.
a+b = b+a
4. El orden de los factores no altera el .producto de números naturales.
a•b = b•a
Propiedades asociativas
5. Para sumar tres o más números naturales no importa el orden.
a+b+c = a+b+c
6. Para realizar el producto de tres o más números naturales no importa el orden.
a•b•c = a•b•c
Propiedad distributiva
7. El producto de un número natural con la suma de dos naturales es igual a la
suma de los productos.
a• b+c = a• b+a• c
Números Enteros (Z)
Al restar dos números naturales el resultado no siempre da un natural, esto quiere decir
que la operación resta no cumple con la propiedad de cerradura, por ello es necesario utilizar “nuevos” números que vienen a complementar los naturales para que se satisfaga la cerradura en la resta, así como en la suma y el producto.
Dichos números se conocen como los Enteros, y son:
(Z)= …- 5, -4, -3, -2, -1,0,1,2,3,4,5,6,7,8,9,10…
Números racionales (Q)
Estos elementos son aquellos números que se pueden expresar como el cociente de dos números enteros, siendo el divisor diferente de cero.
Se denota por el símbolo (Q) y se define simbólicamente de la siguiente forma.
{Q= x tal que x= a/b donde a y b son enteros con b≠0}
Números Irracionales
Son aquellos cuya expresión decimal no es periódica.
Ejemplo de estos números es √2, √3, √5, √7 y en general la raíz cuadrada de un número primo, pues su expresión decimal no es periódica. También son números irracionales como el siguiente:
π: 3.1415926535…
Medidas De Dispersión
¿Qué son las medidas de tendencia central?
Estas dirigen su interés al comportamiento de los datos en relación a un valor central pero se olvidan de la forma en la que los datos varían o se dispersan.
¿Qué son las medidas de dispersión?
Las medidas de dispersión se encargan de estudiar el comportamiento de todos los datos y cómo se distribuyen alrededor de un valor central, la media aritmética. Dentro de las medidas de dispersión se encuentran: el rango, la desviación media, la desviación estándar y la varianza.
¿A qué se refiere el rango?
A la variación o diferencia entre el dato mayor y el dato menor de un conjunto de datos u observaciones se le llama Rango
Por ejemplo una serie de datos cuantitativas, como lo es la estatura, donde en centímetros tendríamos:
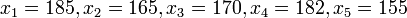Es posible ordenar los datos de la siguiente manera;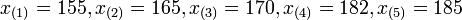Donde la notación x(i) indica que se trata del elemento i-ésimo de la serie de datos. De este modo, el rango sería la diferencia entre el valor máximo (k) y el mínimo; o, lo que es lo mismo: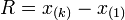En nuestro ejemplo, con cinco valores, nos da que R = 185-155 = 30.
